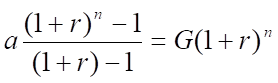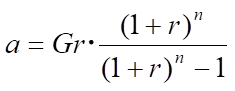数列{[pmath]a_{n}[/pmath]}が、[pmath]a_{1}[/pmath]=3, [pmath]a_{2}[/pmath]=6, [pmath]a_{3}[/pmath]=12, ・・・, [pmath]a_{n}=3[/pmath]・[pmath]2^{n-1}[/pmath]で表されるものを初項3、公比2の等比数列と呼び、一般に初項a、公比r、の等比数列は、[pmath]a_{n}=ar^{n-1}[/pmath]と表され、その和[pmath]S_{n}[/pmath]を等比級数と呼びます。今、試みに[pmath]S_{n}[/pmath]を求めてみると下記、(1)式の両辺にr をかけた(2)式を用意して
[pmath]S_{n}[/pmath]=[pmath]a[/pmath]+[pmath]ar[/pmath]+・・・・+[pmath]ar^{n-1}[/pmath] (1)
[pmath]rS_{n}[/pmath]= [pmath]ar[/pmath]+・・・・+[pmath]ar^{n-1}[/pmath]+[pmath]ar^{n}[/pmath] (2)
r≠1 のとき、(1)式の辺々から(2)を引いて(1)-(2)を計算すると、
[pmath](1-r)S_{n}=a-ar^{n}[/pmath]
[pmath]S_{n}={{a(1-r^{n})}/{1-r}}={{a(r^{n}-1)}/{r-1}}[/pmath]と公式どおり求まりました。
仮に例えば元金G、利息(月利)r、支払回数 n、の車なりマンションを買うとき、ローン返済を組むと、月々の支払いaはいくらになるでしょうか。
毎月、元金に(1+r)の利息を掛けて毎月、aの支払いをn 回した結果、残金がゼロになるので、
整理すると、
左辺は初項a, 公比1+r の等比級数ですから、公式により・・・
したがって
支払い総額G’=anですね。