JavaScriptの座標変換の例

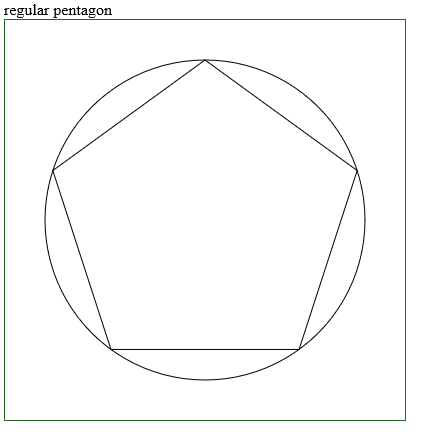
今回はJavaScriptの座標変換を使って正五角形をCanvasに描画してみました。

半径 r の円に内接する正五角形の円の中心から各辺に下した垂線の長さ [pmath]ay={{1+sqrt{5}}/{4}}r [/pmath] , 円の中心を原点として各辺の一辺の長さ[pmath]a=2ax={{sqrt{10-2sqrt{5}}}/{2}}r[/pmath] が既知としています。

https://stuffy.mydns.jp/~gusachan/javascript/pentagon.html

var c=document.getElementById("graph");
var ctx=c.getContext("2d");
var dgr =  Math.PI/180;
function pentagon() {
  var r = 160, ax, ay, bx, by;
  ax = -(Math.sqrt(10 - 2*Math.sqrt(5)))*r/4;
  ay = (1 + Math.sqrt(5))*r/4;
  bx = -ax;
  by = ay;
  ctx.beginPath();
  ctx.save();
  ctx.translate(200 + ax, 200 + ay);
  ctx.moveTo(0,0);
  leg();
  ctx.rotate(-72*dgr);
  leg();
  ctx.rotate(-72*dgr);
  leg();
  ctx.rotate(-72*dgr);
  leg();
  ctx.rotate(-72*dgr);
  leg();
  ctx.closePath();
  ctx.restore();
  function leg() {
    ctx.save();
    ctx.lineTo(2*bx,0);
    ctx.restore();
    ctx.translate(2*bx,0);
  }
}
pentagon();
ctx.stroke();
beginPath();
ctx.arc(200,200,160,0,360*dgr,false);
ctx.stroke();

円の中心を原点として五角形の左下隅の角の座標(ax, ay) =(-(Math.sqrt(10 – 2*Math.sqrt(5)))*r/4, -(1 + Math.sqrt(5))*r/4) をCanvasの座標の（左上隅を(0,0)とする）原点からtranslate(200 + ax, 200 + ay)) して始点とし、leg() 関数を呼び出して底辺を一回描画したのち、restore()で座標系変換を元に戻しtranslate(2*bx, 0)でレグの終点を(0,0) になるように移動してrotate(-72*dgr)で72°反時計回りに回転 、次の底辺の再描画～を4回繰り返してstroke()しています。

テキストではフラクタル雪片を再帰レベル4で描画していました。