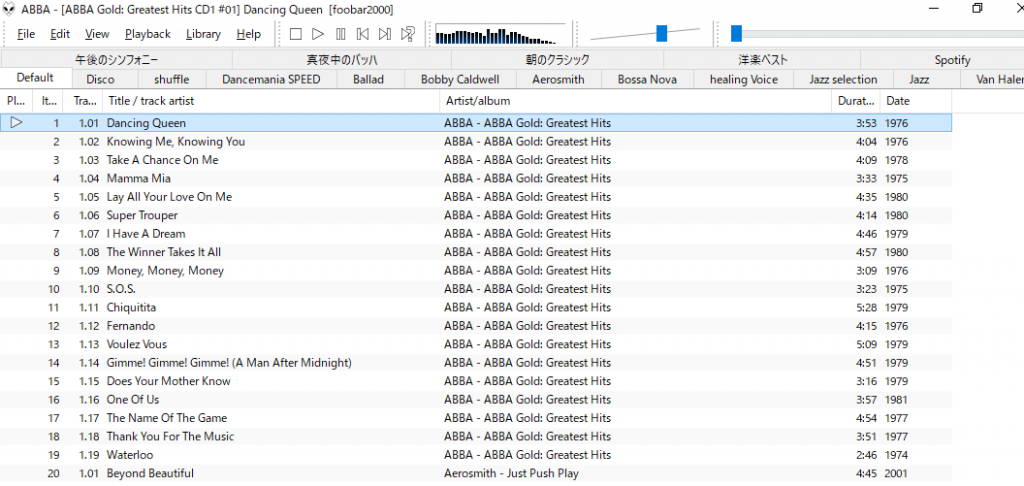
カスタマイズの自由度が高いfoobar2000ですが、カスタムスキンをインストールするにはColumns UI など動作に必要なコンポーネントをあらかじめ用意しなければなりません。しかし幸い、ファイルのダウンロードリンクとインストールの概要が foobar2000&スキンのインストール にありましたので詳細は譲ることとします。
コンポーネントをダウンロード解凍してfoobar2000のインストールフォルダにコピー、初回起動のUIの選択でColumns UIを選択、今回はDeviant ARTの PandoraBox カスタムスキンをダウンロードしました。(英サイト/要ログイン)
1.7zipファイルを 7-zipファイルマネージャー などで解凍。
2、 configuration, FONT, images, scripts, user-components の5フォルダが見えます。その中のFONTフォルダを開いて.ttf拡張子のフォントファイル3個をダブルクリックしてインストール。
3.imageフォルダをC:\Program Files(x86)\foobar2000 の中にコピー。
4.残りのフォルダ(configuration, scripts, user-components)を %appdata%foobar2000 にコピー。
アプリを実行するとカスタムスキンが起動しました。
[File]-[Perferences]の左ペインの[Display]-[Main Window]から[Esc key function] を[Exit] に設定するとfoobar2000 がアクティブウィンドウのときに[Esc]を押すとアプリを終了でき便利です。
最初、席を離れるときにWindowsを[Windows]+[L] でログオフすると音が止まる現象に悩みましたが、[Playback] から[Other] の中の[Prevent screensaver & monitor standby when playing] のチェックを外すと良かったみたいです。
それでは、楽しい「foobar2000」ライフを!